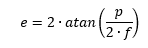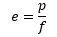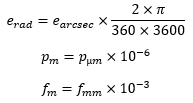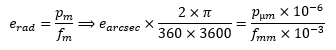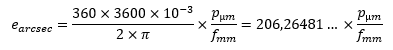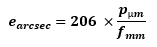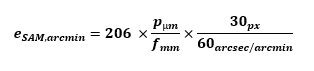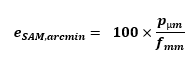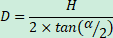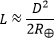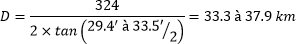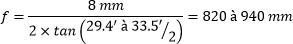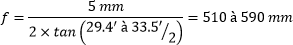-
Compteur de contenus
16810 -
Inscription
-
Jours gagnés
60
Type de contenu
Profils
Forums
Téléchargements
Blogs
Boutique
Calendrier
Noctua
Tout ce qui a été posté par Fred_76
-

Je pense avoir fait une première nationale ou mondiale ! ??
Fred_76 a répondu à un sujet de herve30110 dans On fait une pause
tout à fait, il y a un soucis avec la longueur de l’ombre. -

150/750 ou bien un 200/1000 qui risque de ne pas renter dans mon coffre de voiture ?
Fred_76 a répondu à un sujet de delcencen dans Matériel général
Moi non plus jamais de problème pour mettre le 200/1000 sur la banquette arrière de ma Clio, et même dans une Twingo ça passait (mais une vraie Twingo pas le dernier modèle de m@@@). -

Le refuge de la Cougourde (Mercantour)
Fred_76 a répondu à un sujet de Astropaysages dans Photos de Paysages de nuit
C’est vraiment impressionnant, les nuages apportent effectivement beaucoup à l’ambiance. -

besoin aide choix Sac ados astrophoto
Fred_76 a répondu à un sujet de podline6 dans Matériel astrophotographique
-

besoin aide choix Sac ados astrophoto
Fred_76 a répondu à un sujet de podline6 dans Matériel astrophotographique
En fait les sacs photos se posent rarement debout, on les pose à plat pour accéder au matériel. En randonnée, peu de risque d'éborgner quelqu'un, les randonneurs se baladent généralement l'un derrière l'autre ou 2 à deux, et on fait attention ! Les sacs photos s'ouvrent aussi rarement par le dessus, mais souvent sur le côté, sur la face avant ou arrière. Et pour la gourde, on peut la mettre sur le coté, quitte à en mettre une de chaque coté pour équilibrer le poids. Une gourde pleine, c'est compact et au plus 600 g (1/2 l). Un trépied photo avec la rotule, c'est au moins 2 kg et une grosse inertie. Je préfère donc tout bien équilibrer pour préserver mon dos ! -

Masque Bathinov 250
Fred_76 a répondu à un sujet de turboIII dans Discussions générales de L'impression 3D en astronomie
Sinon avec un cutter et une règle, sur une feuille plastique A3, nickel. -

besoin aide choix Sac ados astrophoto
Fred_76 a répondu à un sujet de podline6 dans Matériel astrophotographique
Je ne comprends pas pourquoi les plupart des sacs à dos photo ne permettent pas de placer le trépied à l’horizontale soit dessus soit dessous le sac. Dans la quasi totalité sinon tous, on peut soit le mettre debout sur le devant du sac, et bonjour le bras de levier sur le dos, soit debout sur le côté et bonjour le déséquilibre latéral… et dans les tests, personne n’en parle ! A croire que les testeurs n’utilisent jamais de trépied ! Sinon pensez à prendre un sac adapté au gabarit cabine si vous voulez le prendre un jour en avion. Notez que le trépied n’est pas accepté en cabine (c’est la soute obligatoire). J’ai le sac Lowepro Whistler BP 350 AW II qui est assez large pour contenir tout le matériel nécessaire à une sortie astro avec Star Adventurer Mini ou Astrotrac, boîtier photo (6D) et 1 objectif, les powertanks et la quincaillerie. Il est compatible cabine avion. Il est parfois en promo sinon on le trouve dans les 300€. J’ai bricolé une sangle pour placer le trépied à l’horizontale au dessus du sac (derrière mon cou). Comme ça les masses sont bien réparties et mon dos me dit merci ! -

Spéculation sur nouveau modèle astrophysique
Fred_76 a répondu à un sujet de bobrun043 dans Astronomie & Astrophysique
A rien, c’était juste pour faire avancer le schimilibilili bililschili scmilbilili… -

Spéculation sur nouveau modèle astrophysique
Fred_76 a répondu à un sujet de bobrun043 dans Astronomie & Astrophysique
Quand j’ai dit ça à ma collègue, elle a pouffé… et m’a répondu que c’était dur à avaler… comme argument bien sûr. -

Spéculation sur nouveau modèle astrophysique
Fred_76 a répondu à un sujet de bobrun043 dans Astronomie & Astrophysique
Tu ne t’appelles donc pas Clair. CQFD -
un peu de lecture : https://sahavre.fr/wp/bruit-part-1/
-
Gratuit Tout est expliqué ici :
-
Utilises plutôt Sequator pour PC ou Starry Landscape Stacker sur Mac qui sont faits pour ça. PI n’est pas fait pour traiter ce genre d’images… ou alors c’est compliqué.
-
Parce que c’était aussi un portail de vente d’Amazon (de nombreux liens dans les tests pointent sur les articles qu’ils vendent) donc en le cédant ou en le revendant ils ouvraient la porte à la concurrence…
-

DEBAT BIAS/BIAS SYNTHETIQUE / FLATDARKS
Fred_76 a répondu à un sujet de 180Vision dans Matériel astrophotographique
Sur les APN, le niveau de décalage, que certains appellent « offset synthétique » est une puissance de 2, constante quelque soit le réglage ISO. Par exemple 256, 512, 1024, 2048. Sauf que certains boîtiers comme le Canon R6 (mk I ou mk II) ont un niveau de décalage qui varie selon le réglage ISO. Il est de 512 jusqu’à 320 ISO et 2048 à partir de 400 ISO. Ça permet de gagner en dynamique, mais il faut bien en tenir compte si d’aventure il vous arrivait de prendre des photos astro a 100 ISO (!). Ce n’est pas ce qu’il dit, enfin pas tout à fait. Il dit que pour les flats, le « flat-dark » ne fait rien gagner, qu’un bias sera meilleur, mais surtout que soustraire le niveau de décalage (offset synthétique) tout simplement sera encore mieux. -
Ce qu’il faut savoir, c’est que DPReview avait été racheté par Amazon en mai 2007. Et Amazon a fait une coupe claire dans ses branches jugées non primordiales à ses intérêts. DPReview en fait partie… voici la justification envoyée aux employés d’Amazon : En conclusion, DPReview fermera ses portes le 10 avril 2023. Si vous aviez publié des revues ou autres articles sur DPReview, vous pouvez demander les données jusqu’au 10 avril à cette adresse : https://www.dpreview.com/data-download
-
Bonsoir ce soir je viens de recevoir un message annonçant la fin du mega forum de discussion sur le matériel photographique « DPReview » qui proposait en outre moult tests de matériels photo… Triste je suis car c’était une grande source de renseignements. a+ Fred
-
Bonjour, Est-ce que quelqu’un connaît ça ? https://www.cloudynights.com/topic/813642-new-free-open-source-ai-denoise-framework-and-gui-tool-astrodenoisepy/ Un développeur vient de mettre ça sur CloudyNights, un debruiteur gratuit dans le genre de TopazDenoise ou BlurXterminator. C’est en cours de développement mais ça semble prometteur car spécifiquement dédié Astro. Peut être une future implémentation dans Siril car le code est libre (mais en Python 😣). Cette image n’est pas de moi mais montre le travail effectué :
-
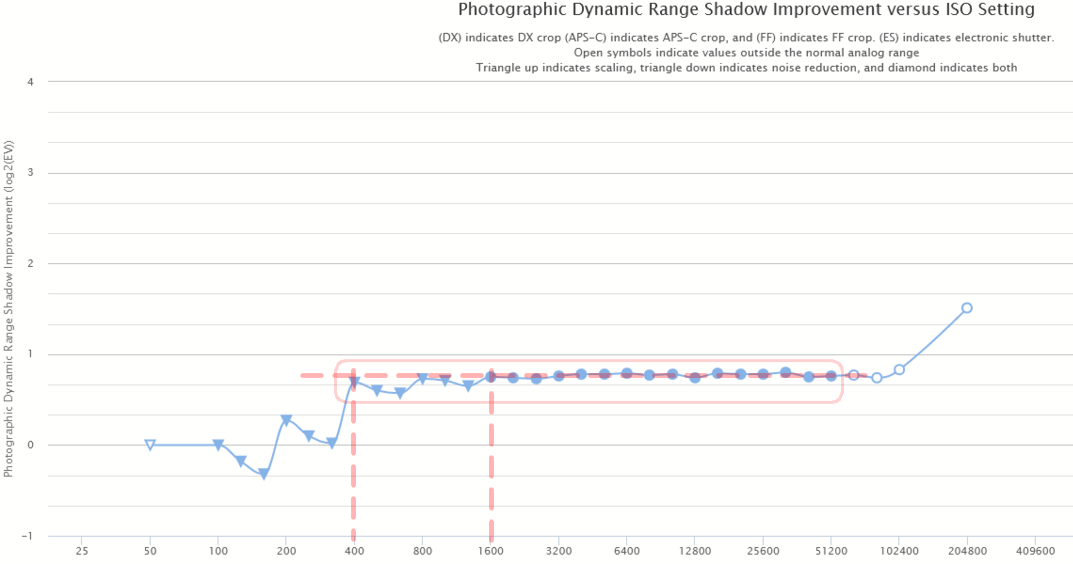
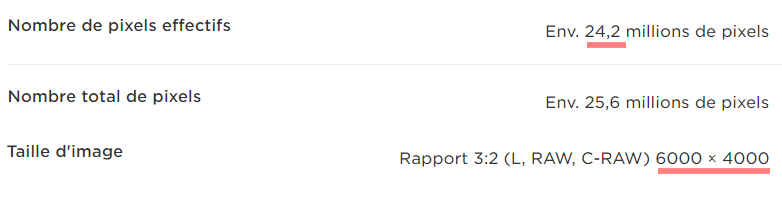
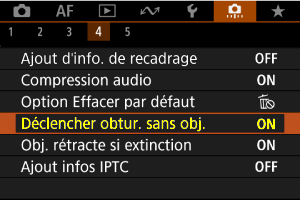
Bonjour Le Canon R6 mark II (ou son petit frère le R6 mk I) est un digne successeur du Canon EOS 6D. Je vais développer plus en détail ce boitier (ce message sera donc modifié au fur et à mesure de mon travail dessus). Boitier Le Canon R6 mk II est de type hybride, aussi appelé "mirror-less", donc sans miroir. Sa monture RF offre un diamètre de 54 mm, identique au diamètre de la monture EF qui équipait les réflex numériques de la marque. Le boitier nu pèse 670 g. Compatibilité avec les objectifs Le boitier est directement compatible avec les objectifs RF, et EF/EF-S avec la bague RF-EF. Notez que les objectifs EF-S (faits pour les APS-C) provoqueront un gros vignettage sur ce capteur plein format. Attention toutefois, Canon semble avoir renforcé sa protection contre les fabricants tiers. Des utilisateurs ont rencontré des gros problèmes en montant un objectif Samyang (ou Rokinon c'est pareil) sur un Canon R6 mark II ou Canon R7. Plusieurs objectifs de cette marque sont incriminés, mais il est probable que tous soient problématiques : - RF 14 mm f/1.8 AF - EF 85 mm f1.4 , EF XP 50 mm f/1.2 , EF 14mm f/2.8 , EF SP 10 mm f/3.5 (avec puce pour l'AF) Le symptôme est un blocage de l'appareil photo qui nécessite de retirer la batterie et de la remettre, voire, avec le RF, de faire un Reset usine de l'appareil photo. Ce problème n'est pas rapporté sur les R, R6 et R5. Il semble que le problème vienne de la puce AF (ou AE) placée sur les objectifs manuels pour faciliter la mise au point. Vous pouvez essayer de couvrir les contacts de la puce pour que l'appareil photo ne communique plus du tout avec l'objectif. Vous n'aurez plus l'assistance de mise au point, mais au moins l'objectif devrait fonctionner. *** mise à jour *** Le firmware 1.1.1 du R6 mark II semble corriger le problème pour les Samyang AF, mais pas les manuel avec puce AE. Pour le R7, le problème sera probablement réglé avec la prochaine version de firmware (actuellement c’est la 1.2.0). Sources : https://www.dpreview.com/forums/post/66461698 https://www.dpreview.com/forums/post/66686661 https://community.usa.canon.com/t5/EOS-DSLR-Mirrorless-Cameras/EOS-R6-Mark-II-Freezes-with-Rokinon-Lens/td-p/396690 Pas de problème à priori sur les objectifs Sigma. Prise de vue sans objectif (sur télescope/lunette) Par défaut, on ne peut pas prendre de photo sans qu'un objectif soit monté, ou quand aucun contact n'est détecté avec l'objectif, ce qui est le cas quand on utilise une bague de montage pour télescope, ou un ancien objectif. Il faut dans ce cas activer l'option de prise de vue sans objectif. Elle se trouve dans le menu C.FN 4 : Distance optique La distance optique est la distance entre le plan du capteur et la platine de montage des objectifs. Comme il n'y a plus de miroir dans les hybrides, celle ci a été réduite à 20 mm (contre 44 mm dans les reflex EF et EF-S). Il faut donc une bague spéciale, vendue 110€ pour adapter les objectifs EF à la monture RF. Je parle plus loin de ces bagues. Capteur Le capteur CMOS est de type "Dual Pixels" propre à Canon, et n'est ni empilé (stacké) ni éclairé par l'arrière (BSI). Sur le papier, Canon indique un capteur d'environ 24,2 MPixels, mais qui produit des images de 6000x4000 pixels : Je ne sais pas comment ils apprennent les multiplications au Japon, car même après avoir bu une bouteille de saké, trempé ma calculatrice dans de la sauce soja, et posé l'opération avec des baguettes, 6000x4000 donne exactement 24 MPix. Bref, c'est un capteur de 24,0 MPix, offrant des images de 6000x4000 pixels, chaque photosite faisant 5,98 µm de côté. La technologie "Dual Pixels" est propre à Canon. Chaque pixel est séparé en 2, ce qui permet de faire une analyse spéciale pour assurer la mise au point quelque soit l'endroit sur le capteur. Ce n'est pas si inutile que ça en astrophoto car la très bonne sensibilité du capteur lui permet d'assurer comme un grand une bonne mise au point la nuit sur les étoiles. A priori, plus besoin de Bahtinov avec un objectif AF. Par contre inutile de sauvegarder les informations Dual-Pixel dans les RAW, ça ne sert à rien en astrophoto, ça dégrade légèrement les photos (un peu plus de bruit) et ça double la taille des fichiers. Alimentation et autonomie Les batteries LP-E6NH sont du même format que celles qui équipaient pas mal de boitiers reflex de la marque (par exemple le 6D). Le boitier est compatible avec toutes les batteries LP-E6*. Le processeur Digic X qui équipe le R6 mk II est très rapide. Même si c'est le même qui équipe le R6 mk I, il a été optimisé pour consommer moins. L'autonomie CIPA (calcul très conservatif, avec batterie LPE6NH neuve) donne une autonomie de l'ordre de 450/760 photos contre 380/510 avec le R6 mk I (le premier chiffre est avec l'utilisation du viseur électronique, le second avec l'utilisation de l'écran LCD, en mode économie d'énergie). En pratique, on peut aller bien plus loin avant d'épuiser la batterie. On peut aussi l'alimenter directement via un powerbank avec mode "PD Power Delivery" sur la prise USB-C. Plus besoin de fausse batterie. Quand l'appareil photo est éteint, ça permet aussi de charger la batterie dans le boitier (uniquement les LP-E6NH, pas les LP-E6 ni les LP-E6N). C'est donc pratique quand on se déplace dans un endroit sans électricité car un Powerbank de 28000 mAh permet plusieurs charges et évite de trimbaler plein de batteries... à 110€ la batterie, ça fait des belles économies ! Fonctionnalités intéressantes Intervallomètre La série EOS R de Canon, dont le R6 mk II fait partie, dispose (enfin) d'un intervallomètre interne. Mais celui-ci est limité à 99 photos; c'est peu pour un timelapse, (ou un nombre infini) et ne permet pas les photos en mode Bulb, donc on est limité à des poses de 30 s en mode M. L'alternative est d'utiliser un intervallomètre externe. Ca ne coûte pas cher mais ça ajoute un truc supplémentaire à transporter, avec des fils en plus et des batteries à gérer, d'où risque d'oubli et de panne supplémentaire. Mode Bulb Ce mode n'est pas une nouveauté. Ce qui est nouveau sur la série R c'est qu'on peut maintenant saisir la durée de la pose Bulb depuis le boitier. Malheureusement cette fonction ne marche que pour une seule pose et n'est pas associable à l'intervallomètre interne. Notez que cette fonction était déjà présente sur des boitiers reflex récents comme les 80/90D, 6/7D mk II, 5D mk IV, 5DS/R... Quand la photo est prise, un compte à rebours s'affiche sur l'écran. Il est très lumineux et ne pouvait apparemment pas s'éteindre sur le R6 mark I. C'est dommage de voir cette info, car non seulement ça éclaire inutilement la zone (si vous voulez être discret, c'est raté), mais en plus ça consomme de la batterie pour rien. Canon dit avoir corrigé le problème sur le R6 mark II, car l'affichage s'éteint quand on appuie sur la touche "Info". C'est vrai. Mais si on reprend une autre pose Bulb dans la foulée, le compte à rebours se réaffiche à nouveau. On peut aussi replier l'écran mais dans ce cas c'est dans le viseur (!!!) que le compte à rebour s'affiche, et le viseur consomme encore plus que l'écran. Il s'éteint là encore quand on appuie sur Info. Il faut donc appuyer à chaque fois sur la touche Info pour l'éteindre... bref ça sert à rien ! La solution sera donc de régler l'écran sur la plus faible luminosité et une fois la séquence de poses longues lancée, de cacher l'écran avec une petite pochette en tissus, bien occultante. Antiflicker La série EOS R de Canon permet d'activer un système qui analyse le scintillement de la lumière et déclenche la photo au bon moment. C'est très pratique pour faire les flats et éviter les bandes sombres quand le temps de pose est assez court. L'activation de ce mode n'a aucune conséquence sur la qualité des photos. Il désactive cependant l'utilisation de la prise de vue en obturateur électronique, mais comme ce mode fait énormément grimper le bruit, il est préférable de s'en passer. Choses à demander à Canon Si on est nombreux à le demander, peut-être Canon décidera d'incorporer dans une évolution du firmware ? - ajouter le mode Bulb à l'intervallomètre => réponse de Canon France : la suggestion a été remontée au groupe, mais il est peu probable que ça soit implémenté - possibilité d'éteindre complétement le compte à rebours de l'écran et du viseur pendant une série de poses Bulb => réponse de Canon France : la suggestion a été remontée à au groupe, on ne sait pas si ça pourra être implémenté, mais on comprend que ça puisse être gênant pour la photo de nuit - augmenter le nombre de prises de vues successives de l'intervallomètre (999 voire 9999 au lieu de 99) => pas de réponse de Canon France à ce jour La page Contact de Canon est ici : https://www.canon.fr/support/consumer_products/contact_support/ Contactez les aussi car plus il y aura de demandes, plus il y aura de chance (sans garantie) que la suggestion entre dans le tunnel des développements futurs, soit dans une maj de firmware (peu probable) soit dans les nouveaux boitiers à venir. Tarif Le Canon R6 mark II est vendu à 2900€, ce sur quoi il est généralement utile d'ajouter 110€ pour la bague d'adaptation EF-RF afin de pouvoir utiliser les objectifs EF (deux autres bagues sont disponibles dont une qui permet l'insertion de filtre, j'en parle dans un post plus loin). Face à la concurrence, le R6 mk II est le plus cher, mais c'est aussi le plus récent. C'est le grand frère du Canon R6. Le R6 a 20 MPix avec des pixels de 6.56 µm. Ses concurrents directs sont les Nikon Z6 mk I et II, et le Sony A7C de 24.3 MPix (Nikon) et 24 MPix (Sony) avec des pixels de 5.94 µm. Voici les prix de lancement (on peut trouver moins cher maintenant sur certains sites) des hybrides 20-24 MPix du marché : - R6 mk I : 2700 € (en 2020) => 2950 € en tenant compte de l'inflation, vendu neuf en ce moment dans les 2300 € - R6 mk II : 2900 € (en 2023) - Z6 mk I : 2300 € (en 2018) => 2600 € en tenant compte de l'inflation, vendu d'occasion dans les 1500 € en ce moment - Z6 mk II : 2200 € (en 2020) => 2400 € en tenant compte de l'inflation, vendu neuf dans les 2350€ en ce moment - A7C : 2100 € (en 2020) => 2300 en tenant compte de l'inflation, vendu neuf en ce moment à 1850€ Vous me direz qu'il y a aussi les Panasonic Lumix S1, S1H, S5, S5K, les Sony A7 I, II et III, A9, I et II, Nikon Z5... et j'en oublie certainement, mais je ne peux pas parler de tout le monde ! Le A7C a une résolution similaire au R6 mk II (24 MPix) et est vendu 1000 € moins cher. C'est le bas de gamme des Sony hybrides plein format (C comme "cheap" ?). Il présente des performances en basse lumière un chouia meilleures, c'est donc un sérieux concurrent au R6 mk II (ou au R6). Mais son autonomie est largement inférieure et l'ergonomie de l'interface Sony jugée très complexe par la plupart des utilisateurs, sans compter le traitement destructeur que Sony applique sur les RAW dans les poses longues (le fameux Star Eater). Il n'est pas "cheap" pour rien ! Si vous commencez la photo, le A7C sera probablement le meilleur choix grâce à l'économie réalisée, à moins que d'autres fonctions des R6/Z6 I ou II ne soient vraiment utiles pour vous. En ce qui me concerne, j'ai une bonne collection d'objectifs et ils sont tous en monture Canon EF. Je fais aussi des photos de sport de glisse. Les fonctions du R6 sont importantes pour mes besoins donc le A7C et les Z6 étaient exclus... Réglage ISO optimal On constate sur la courbe suivante , issue du site de Bill Claff, qu'on ne gagne plus rien en basse lumière à partir de 400-1600 ISO, c'est à dire à partir du moment où la courbe est horizontale : Augmenter les ISO permet peut être de prendre des photos avec des temps de pose plus courts, mais cela a comme inconvénient de réduire la dynamique. Il est donc préférable de s'assurer de prendre des photos avec une dynamique maximale. Celle ci se trouve entre 400 ISO et 1600 ISO. On constate en regardant cette courbe, qu'il est "ISO Less" à partir de 400 ISO jusqu'à 51200 ISO car la courbe est quasi parfaitement linéaire sur cet intervalle. Le traitement du bruit opéré par le processeur interne pour les photos de moins de 1600 ISO est imperceptible sur les images. On est loin des dégâts causés par le Star Eater qui pénalise les capteurs des hybrides Sony. Dynamique Le R6 mk II est sur la courbe rouge pointillée. A 400 ISO, la dynamique est de 13,5 bits. Elle passe à 12,75 bits à 800 ISO, puis 11,75 bits à 1600 ISO. Ensuite on perd logiquement à peu près 1 bit à chaque fois qu'on double les ISO. Données issues du site de Bill Claff. On constate sur ce graphique que tous les boitiers 20-24 MPix récents se valent du côté de la dynamique à partir de 800 ISO. Le Canon 6D est indiqué en gris. Le Canon R6 mk I est indiqué en pointillés rouge, c'est le moins bon de la série. Les 2 Canon R6 I/II sont par contre supérieurs en dynamique par rapport à toute la concurrence à 400 ISO puisqu'ils sont à 13-13,5 bits de dynamique contre à peine plus de 12 bits pour les autres. La réduction de bruit sur les RAW apportée à cette sensibilité chez Canon est invisible, c'est donc à 400 ISO qu'il faudrait idéalement poser pour les photos de nuit et du ciel profond avec les R6 mk I/II sur les objets à forte dynamique (M31, Orion...).
-

Tutoriel : traitement des paysages de nuit
un sujet a posté Fred_76 dans Tutos et Astuces de Paysages de nuit
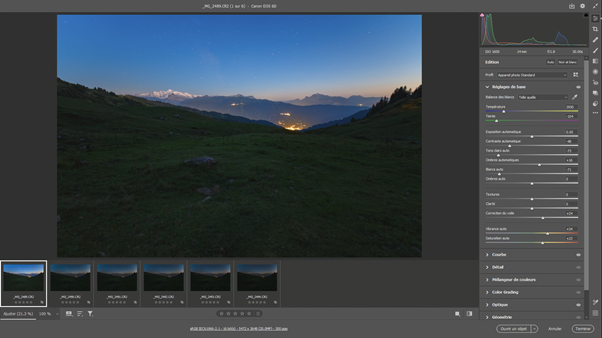
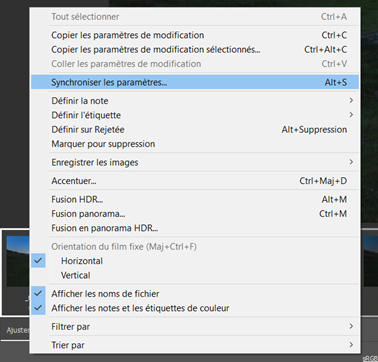
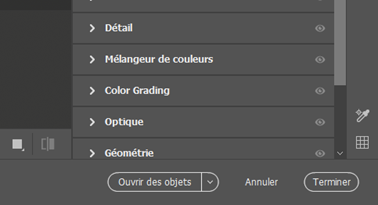
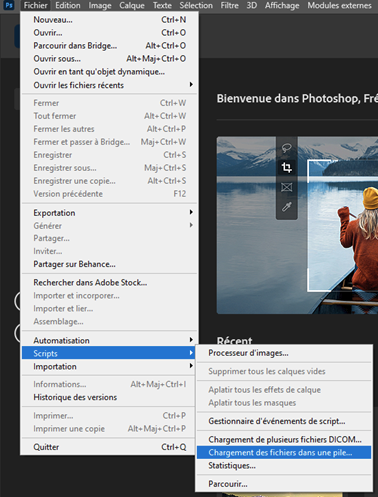
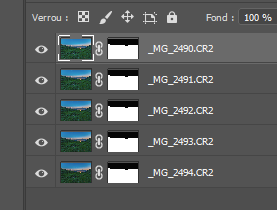
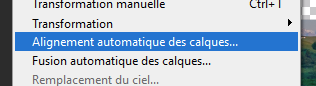
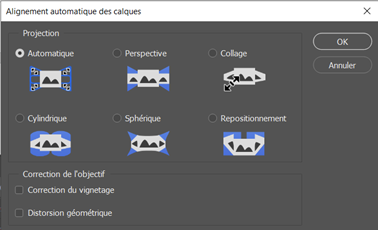
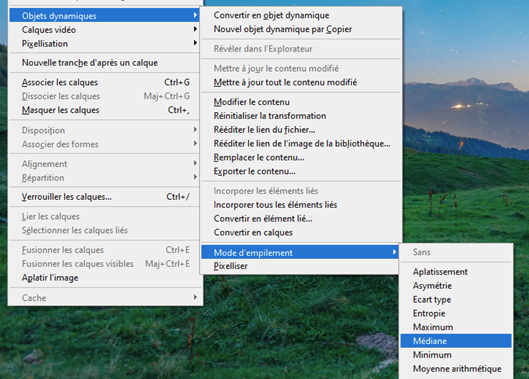
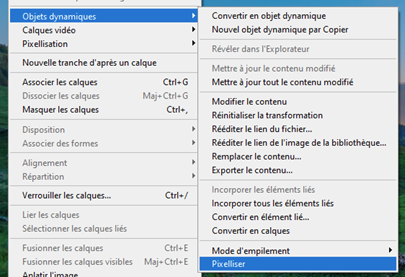
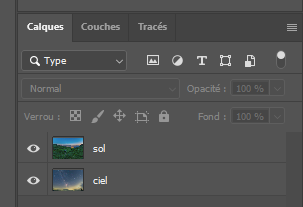
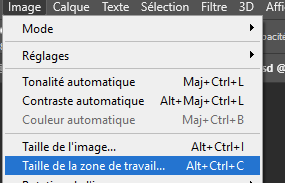
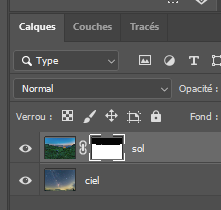
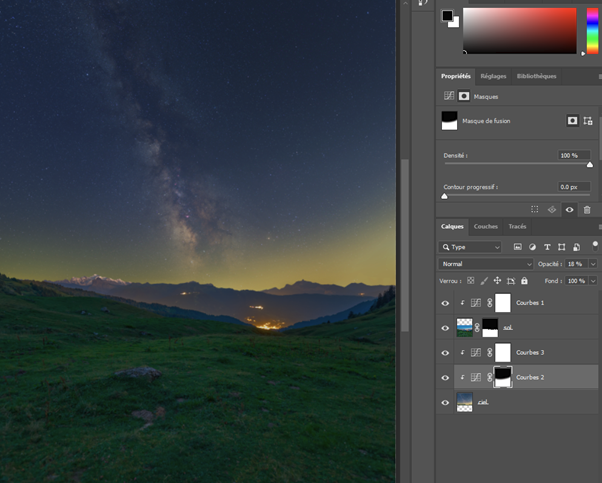
Traitement des paysages de nuit On peut photographier des paysages de nuit de multiples façons, soit avec une pose unique, ou en cumulant plusieurs poses assez courtes pour que les étoiles ne filent pas, ou encore en prenant des poses fixes pour le paysage et d’autres avec suivi pour le ciel. Hormis la pose unique dont le traitement est classique, les poses multiples nécessitent des techniques plus pointues. Ce papier va donner quelques pistes pour traiter les poses multiples. Il ne couvre pas les panoramas. Poses courtes sans suivi C’est la technique la plus simple à mettre en œuvre. L’appareil photo est simplement posé sur un trépied. On règle le temps de pose pour éviter que les étoiles ne filent en utilisant la règle NPF de préférence à la règle des 500. On se retrouve avec un ensemble d’images, généralement entre 5 et 20, inutile d’en prendre tellement plus. C’est la plus simple des méthodes, mais elle impose des temps de pose très courts, d’autant plus courts que la focale est longue. Les images seront donc assez voire très sombres. On rencontre aussi un autre problème lorsqu’on essaye d’empiler des photos sur une longue période : les étoiles tournent, mais pas le paysage. Quand le logiciel va superposer les images en alignant la zone de ciel, il se produira des artéfacts d’autant plus visibles que la durée cumulée est longue. C’est pourquoi il est préférable de ne pas dépasser une durée de l’ordre de 5 minutes entre la première et la dernière pose du paysage. Cette durée sera d’autant plus courte que la focale sera longue mais on peut toutefois mettre à profit les halos de pollution lumineuse au-dessus de l’horizon pour masquer ces artéfacts et augmenter la durée de la séance. N’oubliez pas de faire des darks si le temps de pose unitaire dépasse 5 secondes. Faites aussi des flats si vous utilisez une focale équivalente de plus de 35 mm, en dessous, l’angle de champ est trop large et il est quasiment impossible de faire des flats. Le traitement se fera avec un logiciel spécialisé, comme Sequator pour PC dont un tutoriel dans ce club explique la marche à suivre https://www.webastro.net/forums/topic/168956-tutoriel-sequator-photos-de-paysages-de-nuit/ , ou Starry Landscape Stacker https://sites.google.com/site/starrylandscapestacker/home pour Mac OS. Ensuite vous utiliserez un logiciel de retouche photo pour équilibrer les couleurs, contrastes, etc. Poses courtes avec suivi à la moitié de la vitesse sidérale Cette technique se trouve à mi-chemin entre les deux autres, tant dans son fonctionnement que dans la maîtrise des logiciels de traitement d’images. On doit utiliser une monture équatoriale pour suivre le mouvement des étoiles, mais à la moitié de la vitesse sidérale. Le temps de pose maximal sera le double du temps de pose préconisé par la règle NPF. Grace à cet artifice, le paysage lointain ET les étoiles seront globalement nets, même si d’une photo à l’autre les étoiles se déplaceront par rapport au paysage. Notez que le paysage proche souffrira d’un flou de mouvement, d’autant plus qu’il sera proche de vous et sur les bords de l’image. C’est pourquoi cette technique est surtout utilisable avec les cadrages sur des paysages lointains et des focales de 24 m ou plus. Comme le paysage va lentement pivoter, l’utilisation des logiciels comme Sequator ou Starry Landscape Stacker ne sera pas possible directement car ils s’attendent à ce que le paysage soit fixe. C’est pourquoi il faut commencer par aligner les images sur le sol. 1. Ouvrir toutes les photos depuis Photoshop. Camera RAW se lance et s’ouvre sur la première photo du groupe. Régler les couleurs, contraste, niveaux, etc. comme vous le souhaitez. Vous pouvez corriger le vignettage et le chromatisme de l’objectif MAIS EN AUCUN CAS corriger les déformations, cela générerait un moiré très disgracieux à l’empilement. 2. Une fois les bons réglages trouvés, synchronisez toutes les images avec ces réglages. 3. Cliquez maintenant sur Terminé (et non pas sur Ouvrir). Cela va générer les fichiers des réglages pour chaque photo. 4. Dans Photoshop, allez dans Fichier > Scripts > Chargement des fichiers dans une pile. Contentez vous d’ouvrir simplement les fichiers sans les aligner. Les fichiers s’ouvrent chacun dans un calque séparé. 5. Retirez les traces d'avions et de satellite sur chaque image individuelle, c'est bien plus efficace et rapide à ce moment que de le faire sur l'image finale. 6. Pour chaque calque, ajoutez un masque de fusion et masquez le ciel. Inutile d’être très précis. 7. Sélectionnez tous les calques et aligner les avec la commande Edition > Alignement automatique des calques. Utilisez le mode « automatique » mais ne corrigez pas la distorsion (avec les grands angles ça donne des choses bizarres). 8. Après un temps de calcul conséquent, tous les calques seront alignés sur le sol. Supprimez tous les masques de fusion. 9. Sauvez chaque calque dans un fichier avec Fichier > Exportation > Exporter les calques dans des fichiers. Choisissez le format TIF 16 bits en conservant le profil ICC. On se retrouve dans le Cas 1, mais avec des temps de pose admissibles doublés et sans flou excessif. Vous pouvez maintenant aligner et empiler ces images avec Sequator ou Starry Landscape Stacker puis avec un logiciel de photo pour le reste. Poses séparées : sol sans suivi, ciel avec suivi C’est la technique la plus complexe. Elle n’est pas à la portée des débutants en traitement d’images. Il est nécessaire de bien maîtriser les techniques de calques et des masques dans votre logiciel de traitement d’images. Vous êtes prévenus ! Afin de faciliter la phase de post traitement, éviter - dans la mesure du possible - de cadrer dans votre paysage des zones boisées, des structures aérées (pylônes, bâtiments resserés...) car ils compliqueront sérieusement le travail de détourage (cf. étape 4 de l'assemblage ciel/paysage). On prend une première série d’images en cadrant le sol, sans mettre en marche la monture astronomique. Puis on prend une deuxième série pour le ciel, en recadrant éventuellement l’image vers le haut afin de capter plus de ciel. Il faut cependant garder suffisamment de paysage pour pouvoir ajuster correctement les deux séries l’une à l’autre. La série du sol sera exposée de façon à bien distinguer les détails du paysage. Idéalement il est préférable de faire cette série pendant l’heure bleue ou pendant le crépuscule ou l’aube, de façon à avoir un léger éclairage naturel sur le paysage. En général il n’est pas utile de prendre des darks sur cette série car on a plein de signal. La série du ciel sera exposée pour maximiser le signal, ce qui est possible grâce à la monture qui va compenser la rotation de la Terre. L’augmentation du temps de pose permet de fermer un peu l’objectif et de le régler à une ouverture qui minimise les aberrations optiques (chromatisme, coma…) et le vignettage. Par exemple je ferme le Sigma Art 14/1.8 à f/2.2 pour quasiment supprimer la coma. On peut aussi baisser les ISO. Attention à ne jamais surexposer les zones du ciel, surtout celles impactées par la pollution lumineuse, ou certaines nébuleuses. Avec les grands angles (24 mm ou moins), il est difficile voire impossible de faire des flats corrects. Vous devez en revanche faire des darks. Au sujet des flats en grand angle Avec un grand angle, faire des flats devient problématique car le champ couvert par l'objectif est très large. L'écran à flat doit non seulement bien recouvrir tout le champ cadré mais aussi assurer une lumière uniforme, autant au centre de l'image que sur les bords. Or comment faire un écran à flat qui assure cette uniformité ? L'objectif voit les rayons venir dans un large secteur de sphère devant lui, il faudrait donc que l'écran à flat soit sphérique pour que les rayons lumineux arrivant au centre de l'image aient la même intensité que ceux qui arrivent des bords. Si on utilise un écran à flat plan, le trajet optique des rayons situé au centre de l'image sera plus court que celui des rayons qui arrivent des bords. Ces derniers seront donc plus sombre, non pas à cause du vignettage, mais à cause de cet écart de distance. Le flat obtenu ne corrigera pas correctement le vignettage et corrigera de façon excessive les bords de l'image qui apparaîtront donc plus clairs. Voici un exemple. J'ai pris, de jour, une photo d'un paysage avec un 14 mm sur un plein format. L'image est très vignettée. J'ai ensuite fait des flats avec un écran à flat de format A5 posé au plus prêt de l'objectif (sur son pare soleil). Les photos ci dessous montre le résultat : - en haut à gauche, la photo non corrigée - en haut à droite, la photo corrigée avec le profil d'objectif dans Adobe Camera Raw - en bas à gauche, le flat utilisé - en bas à droite, la photo corrigée avec le flat (j'ai utilisé Sequator) On constate que la correction apportée avec le profil de l'objectif est parfaite, alors qu'avec le flat manuel, les bords sont sur-corrigés. Sachant que faire des flats impose un matériel spécifique (écran à flat, batterie...), un post traitement particulier, et du temps, autant ne pas en faire du tout et laisser faire la correction du profil de l'objectif ! Traitement de la série du sol (sans suivi) Ce traitement vise à augmenter le rapport signal sur bruit. Si de la flexion, des vibrations ou des facteurs extérieurs ont provoqué un déplacement de l’axe de visée, on peut aussi profiter de cette étape pour réaligner les images. 1. Ouvrir toutes les photos depuis Photoshop. Camera RAW se lance et s’ouvre sur la première photo du groupe. Régler les couleurs, contraste, niveaux, etc. comme vous le souhaitez. Vous pouvez corriger le vignettage et le chromatisme de l’objectif MAIS EN AUCUN CAS intervenir sur la géométrie (correction des déformations de l’objectif, redimensionnement, pivoter), cela générerait un moiré très disgracieux à l’empilement. 2. Une fois les bons réglages trouvés, sélectionnez toutes les images dans le bandeau en bas, puis synchronisez toutes les images avec ces réglages. 3. Cliquez maintenant sur Terminé (et non pas sur Ouvrir). Cela va générer les fichiers des réglages pour chaque photo. 4. Dans Photoshop, allez dans Fichier > Scripts > Chargement des fichiers dans une pile. Contentez-vous d’ouvrir simplement les fichiers sans les aligner. Les fichiers s’ouvrent chacun dans un calque séparé. Si vous n’avez pas besoin d’aligner les photos, passez directement à l’étape 8. 5. Pour chaque calque, ajoutez un masque de fusion et masquez le ciel. Inutile d’être très précis. 6. Sélectionnez tous les calques et aligner les avec la commande Edition > Alignement automatique des calques. Utilisez le mode « automatique » mais ne corrigez pas la distorsion (avec les grands angles ça donne des choses bizarres). 7. Après un temps de calcul conséquent, tous les calques seront alignés sur le sol. Supprimez tous les masques de fusion. 8. Sélectionnez tous les calques et convertissez-les en objet dynamique avec la commande Calque > Objets dynamiques > Convertir en objet dynamique. Cette opération va durer très longtemps. 9. Calculez la médiane avec la commande Calque > Objets dynamiques > Mode d’empilement > Médiane. 10. Aplatissez l’image avec la commande Calque > Objets dynamiques > Pixelliser Vous pouvez maintenant sauver la photo dans un fichier PSD que vous appellerez « sol ». Traitement de la série du ciel (avec suivi) Ce traitement vise à aligner les étoiles (et la Voie Lactée) et à augmenter le rapport signal sur bruit. Là, pour le coup, Photoshop ne fait généralement pas du bon travail. L’alignement des photos sur le ciel est souvent raté et quand on empile les photos ainsi alignées, on se retrouve avec une image peu convaincante. Heureusement il y a des alternatives, comme Sequator et Starry Landscape Stacker qui savent traiter les images contenant une partie de sol (ce n’est pas le cas des logiciels dédiés au ciel profond comme Iris ou Siril). Comme on traite des images avec assez peu de signal, il est préférable d’exploiter les darks et éventuellement les flats. Alignement avec Sequator ou Starry Landscape Stacker Si vous utilisez un PC, je vous recommande d’utiliser Sequator. Le tutoriel est ici. Je n’ai pas de Mac pour donner la procédure avec Starry Landscape Stacker. Pour les deux logiciels, inutile d’optimiser quoique ce soit pour le sol, il sera flou, concentrez-vous sur le ciel. Une fois l’image calculée, ouvrez la avec votre logiciel photo pour équilibrer les couleurs, contrastes… selon vos goûts et surtout selon votre expérience, puis sauvez le résultat sous le nom ciel.tif. Assemblage du ciel et du paysage Vous avez deux images, l’une avec le paysage terrestre, l’autre avec le ciel. Il faut les assembler pour retrouver le paysage de nuit que vous avez photographié. Dans Photoshop ou n’importe quel logiciel photo gérant les calques : 1. Ouvrez chaque image dans un calque séparé. Le calque « ciel » sera sous le calque « sol ». 2. Augmentez la taille de la zone de travail vers le haut pour donner de la place au ciel. 3. Réglez la transparence du calque sol à 50% environ, pour voir le ciel en dessous et déplacez le ciel pour que le sol (à peine) visible (car il est flou) soit à peu près aligné sur le sol net : 4. Masquez le ciel sur l’image du sol. C’est la partie la plus délicate, surtout si des éléments très détaillés du paysage, comme des arbres ou des pylônes électriques, des bâtiments, etc., se détachent sur le ciel. Il faut être très méticuleux. Plein de tutoriels existent sur le net pour le masquage des zones complexes d’images de paysages de nuit, mais la plupart, sinon tous, sont en anglais. 5. Le résultat est généralement horrible, le sol flou présent sur l’image du ciel bavant intégralement au-dessus de l’horizon. 6. Il faut alors un peu pivoter le calque du ciel. Le pivotement n'est pas tricher avec la réalité à condition de faire en sorte que la Voie Lactée se trouve quelque part entre ses positions extrêmes de la première à la dernière image de la série : À moins de passer beaucoup de temps (et en plus ce n'est pas simple à faire) à recouvrir les zones floues du paysage à coup de tampon de duplication, vous avez la possibilité de déplacer le ciel vers le bas de quelques dizaines de pixels pour que les zones souillées par l’image floue du sol, disparaissent sous l'horizon. Là pour le coup, on tord la réalité, et il faut donc le faire avec mesure au risque de fabriquer une chimère. L’alternative "pure" est la pose unique en suivant la règle NPF, mais il faudra oublier tous les détails dans la Voie Lactée et dans le paysage. 7. Souvent il est possible que certaines zones ne soient pas dissimulables, par exemple à droite sur cette image. On n’a pas d’autre choix que de recadrer l’image pour éliminer cette partie. Certains n’hésitent pas à redimensionner le calque ciel pour faire sortir les zones floues hors du cadre, mais c’est trop déformer la réalité, je ne préconise donc pas du tout cette façon de faire. 8. S’il reste des traces de sol flou sur l’image du ciel que vous ne pouvez pas masquer par le sol net, vous pouvez aussi utiliser le tampon de duplication (manuel ou automatique) pour les effacer. Il faut être très habile pour que l’intervention ne soit pas visible. 9. Ajustez les réglages de luminosité/contraste/couleur/etc. des deux calques pour qu’ils soient bien homogènes l’un par rapport à l’autre. Avoir un ciel très sombre sur un paysage de jour n’est pas naturel du tout, l’inverse non plus. Évitez aussi de saturer les couleurs, ou de forcer la luminosité et le contraste de la Voie Lactée. Restez réalistes, à moins de faire de l'art : C’est là que votre habileté à manipuler les images avec votre logiciel de retouche photo préféré sera la plus utile et ce n’est pas un simple tutoriel qui peut donner la recette miracle… il faut expérimenter maintes voire moulte fois. N’hésitez pas à utiliser des filtres comme ceux de la Nik Collection (surtout Viveza et DFine), ou encore HLVG… 10. Une fois le résultat acceptable, aplatissez les calques. Recadrez l’image pour supprimer les bords remplis d’artéfacts, et exportez l’image dans le format qui vous convient pour sa diffusion. Résultat final Voie Lactée au dessus du Mont Blanc depuis le col de Joux-Plane, Haute Savoie, un soir d'août. Photo Fred_76 : -
Bonjour à tous, J'ai en projet de faire un module basé sur Arduino qui réalise 2 fonctions : intervalomètre et dithering entre les poses. Il est destiné à être installé sur une monture ayant une entrée ST4. Pas d'ordinateur, pas de grosse batterie, juste un écran LCD, quelques boutons et 3 câbles pour brancher le tout (alim, APN et monture). Alors je vois certains qui me diront : pourquoi seulement ça et pas d'autoguidage ? La réponse est que : je veux du simple. On pose la monture, on fait la mise en station, on cadre et on shoote. Pas de prise de tête avec une caméra d'autoguidage, la recherche d'étoiles guide et les ajustements d'autoguidage & co. Par contre le dithering est absolument nécessaire pour faire des photos potables. La solution doit prendre en compte le dithering en AD uniquement vu que les montures auxquelles il est destiné n’ont pas de motorisation en DEC. Il ne me reste qu'à bricoler le tout ! Mais si d'autres ont déjà fait ce type de montage, histoire de ne pas réinventer le fil à couper le beurre, c'est l'occasion d'en parler ici 😉 Les paramètres à prendre en considération sont : Optique et acquisition - ouverture de l'optique - focale de l'optique (en mm) - taille des photosites du capteur (en µm) Monture - facteur de sur/sous vitesse ST4 (généralement 0,5 mais ça peut être paramétré différemment selon les montures et le choix sur la raquette, par exemple 0.25, 0.75, 1.00 *) - nombre de pixels de dithering Avec ces paramètres on peut calculer : - la durée maximale de dithering (cf. détails dans mes réponses plus bas) Le protocole ST4 fonctionne en tout ou rien. Donc si on donne l'ordre d'aller plus vite en AD, la monture va simplement tourner plus ou moins vite (de 1x ou 0x la vitesse sidérale généralement, mais certaines montures permettent d'avoir un contrôle sur cette vitesse depuis la raquette) jusqu'à ce qu'on arrête de donner l'ordre. On peut donc juste contrôler la durée du dithering. Ensuite on saisi les paramètres de la prise de vue - délai avant de lancer la séquence (en s) - nombre de poses - durée d'une pose (en s) - attente entre la fin du dithering et la pose suivante (en s), ça permet de laisser le temps à la monture de se stabiliser - nombre de poses entre deux dithering - temps d'attente après la levée du miroir avant de prendre la photo (dans le cas où on a activé l'option sur son boitier) Toutes les valeurs devront être stockées pour ne pas avoir à les ressaisir à chaque fois. Développements ultérieurs possibles : - dithering en AD+DEC => cela dit, comme le Dithermeter est surtout destiné aux petites montures ultraportables qui ne suivent qu'en AD, ce n'est pas du tout la priorité. - enchaîner des séries avec des temps de pose différents => mais ça risque de compliquer inutilement l'interface... pas prioritaire non plus - capteur de proximité pour n'allumer l'écran LCD que lorsqu'on est à côté du boitier, histoire d'économiser les batteries => j'ai reçu le capteur VL53L0X, la carte mère a déjà les trous prévus pour le brancher, yapuka programmer et tester, cela dit cette puce microscopique impose un driver énorme pour l'Arduino et prend beaucoup de place en mémoire... Voilà ! A+ Fred
-

Pourquoi l’échantillonnage est égal à 206 p /f ?
un sujet a posté Fred_76 dans Tutos et Astuces de Paysages de nuit
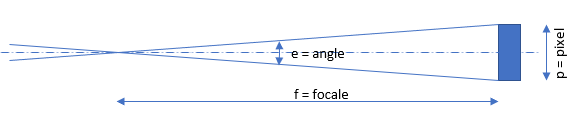
Pourquoi l’échantillonnage est égal à 206 p /f ? Des colistiers se demandent parfois d’où sort ce chiffre de 206 dans la formule qui donne l’échantillonnage d’un capteur en fonction de la taille des pixels et de la focale de l’optique. La réponse est simple : parce que la 206 était une bagnole vraiment cool. C’est bon, vous êtes satisfait ? Non… En fait il y a une explication mathématique mais elle est bien moins cool. La voilà quand même. C'est juste de la trigonométrie de base et un peu de conversion d'unités. Tout d'abord voici le schéma qui montre le principe : L’angle e que voit un pixel de dimension p derrière une optique de focale f est : Ici e est exprimé en radian, p et f dans la même unité de longueur (normalement en mètre) et atan est la fonction arc tangente. Comme p est généralement très petit devant f, le ratio p/2f est proche de zéro. On peut alors simplifier l’expression car atan x est quasiment égal à x quand x tend vers zéro. Il reste alors l’expression : Mais ici, e est toujours exprimé en radian et p et f en mètres. Or on a plutôt l'habitude d'exprimer e en seconde d’arc, p en micron et f en millimètre. Il faut convertir : On a donc : d'où : que l’on s'empresse d'arrondir parce que les décimales ici n’ont aucun sens pratique et on trouve la bagnole très cool : CQFD Gamme de tramage dans la Console SAM/SA L'application qui permet de piloter la Star Adventurer Mini et la Star Adventurer 2i permet la saisie d'un paramètre appelé 'Gamme de tramage'. C'est ce paramètre qui permet de faire du dithering. Il est vraiment IMPORTANT de l'activer. Mais quelle valeur faut-il saisir car le manuel n'en parle pas du tout ? La pratique montre qu'il faut largement exagérer le dithering pour qu'il soit efficace sur ces montures. On estime que 30 pixels de décalage est suffisant. La valeur à saisir dans l'application est en minutes d'arc : Finalement il suffit de retenir la formule simple, valable uniquement pour la SAM et la SA 2i dans l'application Console SAM/SA : (j'ai pas mis 103 parce que la Peugeot 103 n'était pas cool comme mob). -
Comment fonctionne le dithering avec la Star Adventurer Mini ? On est en droit de se poser la question puisque depuis la version 3.10 du firmware de la SAM, une option "Gamme de tramage" (dithering) est apparue dans la SAM Console. Or rien n'est détaillé dans le manuel, dans le texte accompagnant la mise à jour ou encore sur les sites de Skywatcher. Après avoir posé la question à de multiple reprises, voici la réponse de Sky Watcher : Et la traduction en français : En gros voici ce que cela fait. La première photo est prise normalement. Un décalage en + ou en - est appliqué aléatoirement par rapport à la position théorique de la seconde photo. Il se fait dans l’intervalle de temps qui sépare la première de la deuxième photo. Un autre décalage en + ou en - est appliqué aléatoirement par rapport à la position théorique de la troisième photo. Et ainsi de suite. Ils ne précisent pas comment calculer la valeur à entrer dans la case "Gamme de Tramage (Arcmin)", ni combien de temps cela prend à la monture pour se déplacer et se stabiliser pendant et après un dithering, donc combien de temps il faut laisser entre deux poses. Je n'ai pour l'instant pas de réponse à ces questions. Alors ce qui suit est à prendre avec précaution... Si l'on considère un dithering de +/- 10 pixels sur la photo, la formule qui permet de calculer la valeur à entrer est : d (arcmin) = 35 x p (µm) / F (mm) Par exemple avec un Canon 500D (p = 4.68 µm) et une focale de 150 mm, il faudrait saisir 35x4.68/150=1.1 minutes d'arc qu'on arrondira à 1 minute d'arc (c'est la plus petite valeur qu'on peut saisir). edit : Après pas mal d'essais, je me suis rendu compte que le dithering ne commençait vraiment à donner des résultats qu'à partir de 4'. En dessous, ce n'est pas convaincant. Testé avec 135 et 150 mm de focale. Donc il suffit de mettre la valeur 4 dans la case "Gamme de tramage" et de ne plus la changer. Si la monture s'arrête pour faire un dithering "en reculant" ou avance à 2 fois la vitesse sidérale pour aller "en avançant", il lui faut 4 secondes pour se décaler de 1 minute d'arc. Si le décalage précédent était à l'opposé du décalage à appliquer et les deux décalages au maximum de la valeur entrée, l'écart est égal à 2 fois la valeur saisie. On doit aussi laisser le temps à la monture pour qu'elle retrouve son équilibre après cette interruption ou accélération du suivi, disons 5 bonnes secondes. Il faudrait donc saisir un délai entre deux poses tel que : t (s) = 8 x d (arcmin) + 5 s edit : j'ai constaté que 4 secondes d’intervalle entre deux poses était suffisant, pour un dithering de 4'. Par exemple, pour le Canon 500D avec 150 mm de focale, il faudrait saisir un intervale entre poses de 8x1+5=14 s. On arrive rapidement à des valeurs très importantes si la focale est faible et les pixels sont gros, et on fini par perdre beaucoup de temps à attendre le dithering. Il faut donc peser le pour et le contre. En pratique, on à du mal à distinguer le bruit "télégraphique" sur les focales inférieures à 100-150 mm, inutile d'activer le dithering. Ca ne devient nécessaire que pour les focales supérieures à 150-200 mm (et encore...).
-

Tutoriel : la Lune aussi grosse que la Tour Eiffel
un sujet a posté Fred_76 dans Tutos et Astuces de Paysages de nuit
Prendre une photo de la Tour Eiffel contenue dans la Lune, possible ou non ? L'idée de cet article n'est pas de faire cette photo, qui n'est qu'un photomontage à la va-vite, mais de cadrer quand la Lune à la même taille que la Tour Eiffel. Où se placer, quelle focale utiliser, quand prendre la photo ? À quelle distance se placer ? La Tour Eiffel mesure 324 m à la pointe de son antenne. La Lune mesure entre 29.4 et 33.5 minutes d’arc (angle apparent). Il faut se placer à une distance telle que : Où : · H est la hauteur de l’objet qui doit faire la même taille apparente que la Lune · α est l’angle apparent de la Lune · D est la distance à laquelle il faut se placer Avec les données indiquées on a : La Lune se couchant vers l’Ouest, l’un des meilleurs endroits où se placer serait en haut d’une des attractions de Disneyland Paris à 35 km de la Tour Eiffel, idéalement depuis la Tour de la Terreur qui culmine à 66 m, ou d'une autre attraction plus basse mais à la vue dégagée vers Paris. Malheureusement, le relief sur le chemin remonte trop pour voir le bas de la Tour Eiffel, on ne la verra au mieux qu’à partir du 1er étage. Ci-dessous le relief simulé par le site Geoportail.gouv.fr. Mais cette simulation ne tient pas compte de la rotondité de la Terre. Plus on est éloigné, plus l’objet observé disparaît sous l’horizon. La hauteur masquée se calcule assez facilement avec la relation : Où : · D est la distance à l’objet, en m · R⊕ est le rayon de la Terre = 6 371 000 m · L est la hauteur masquée sous l’horizon, en m À 35 km de distance, les objets « s’enfoncent » donc en apparence de 94 m. À l’exception des platistes, on ne verra la Tour Eiffel qu’au-dessus de son 1er étage. La réalité est légèrement différente à cause de la réfraction atmosphérique qui peut faire « remonter » les objets lointains au-dessus de l’horizon. Il peut aussi y avoir des immeubles et arbres entre les deux points qui masquent la vue, Geoportail ne donne que le relief naturel. Bref, il est important de faire des repérages sur place pour vérifier que le point de vue est correct. Par exemple depuis la Cabane des Robinson, on voit bien la Tour Eiffel, mais comme la cabane n'est qu'à 25 m de haut, on voit moins bien la tour que depuis un endroit plus élevé : (extrait d’une photo de Maxfan, 2012) Malheureusement, une antenne téléphonique a été construite dans l’axe, comme le montre cette photo plus récente prise à peu près du même endroit : (extrait d’une photo de Jeff Lang, 2016) Le Panoramagique offre lui aussi une vue sur la Tour Eiffel. Il existe des bâtiments des les villes voisines capables d'avoir un point de vue plus dégagé. À vous de les chercher ! Quelle focale utiliser ? Prenons par exemple le boitier Nikon D850 avec ses 45 megapixels (capteur plein format de 8256x5504 pixels). Pour que la Tour Eiffel (ou la Lune) occupe le tiers de l’image en orientation paysage, soit 8 mm sur le capteur, ou 1835 pixels, il faut une focale telle que : Où : · h est la taille de l’objet sur le capteur · α est l’angle apparent de l’objet vu depuis l’endroit où la photo est prise · f est la focale à utiliser C’est beaucoup mais pas impossible. Cela impose d’utiliser un téléobjectif allant jusqu’au moins 500 mm de focale auquel on ajoute un doubleur. Le Canon 7D mk II a un capteur APS-C de 15x22.4 mm pour 5472x3648 pixels. La focale requise pour que la Lune occupe le tiers de l’image, ou 1216 pixels (donc 15/3=5 mm sur le capteur) est donc : Un téléobjectif allant jusqu’à 600 mm de focale suffirait, mais l’image serait moins résolue (1216 px contre 1835 avec le D850). Quand prendre cette photo ? PhotoPills calcule les créneaux suivants, et voici quelques simulations : 3 janvier 2020 à 0h35, le quartier de Lune sera à moitié derrière la Tour Eiffel 5 mai 2020 à 5h38, presque pleine au-dessus de la Tour Eiffel 11 mars 2020 à 8h19, presque pleine Lune en haut de la Tour Eiffel 8 août 2020 à 11h14, 3 quart au-dessus de la Tour Eiffel 29 octobre 2020 à 4h49, presque pleine Lune au-dessus de la Tour Eiffel 12 novembre 2020 à 16h11, ce sera un fin croissant juste derrière la Tour Eiffel 2 février 2021 à 10h44, lune au ¾ centrée en haut de la Tour Eiffel 25 août 2021 à 09h57, la Lune sera presque pleine et derrière la Tour Eiffel 19 mars 2022 à 07h38, la Lune sera presque pleine et derrière la Tour Eiffel 17 décembre 2022 à 13h31, quart de Lune au-dessus de la Tour Eiffel 9 mars 2023 à 8h08, la Lune sera presque pleine et derrière la Tour Eiffel 15 mai 2023 à 16h25, croissant en haut de la Tour Eiffel 5 août 2023 à 10h59, donc dans la journée, et la Lune sera aux ¾ et au-dessus de la Tour Eiffel Malheureusement aucune de ces dates ne se passe de nuit dans les 5 minutes qui suivent chaque heure du coucher du Soleil jusqu'à 1h05 du matin, on ne pourra donc pas cadrer la Lune avec la Tour Eiffel scintillante. Il reste à : avoir une bonne météo éventuellement avoir l'autorisation du parc pour photographier pendant les heures de fermeture... Et depuis l'Ouest parisien ? En se plaçant à l’Ouest de la Tour Eiffel, on obtient un beau panorama depuis les coteaux de Chènevière / Mézy-sur-Seine. La route d’Apremont semble un bon spot d'après Google Street View. De là, on peut voir la tour Montparnasse, la Tour Eiffel et l’ensemble des gratte-ciel de la Défense. (Photo 2014 Agence B. Folléa - C. Gautier paysagistes urbanistes / DRIEE-IF / Conseil Général des Yvelines) La Tour Eiffel se trouve à 35 km. Les dates où la Lune se lèvera sur la Tour Eiffel sont : 5 novembre 2019 à 15h14 30 décembre 2019 à 11h47 21 mars 2020 à 6h19 19 décembre 2020 à 12h35 5 mai 2021 à 4h40 5 novembre 2021 à 8h24 30 décembre 2021 à 4h45 29 mars 2022 à 7h07 19 juin 2022 à 1h45 26 octobre 2022 à 9h44 20 décembre 2022 à 5h07 11 mars 2023 à 23h37 -

Tutoriel : faire la mise au point de nuit
un sujet a posté Fred_76 dans Tutos et Astuces de Paysages de nuit
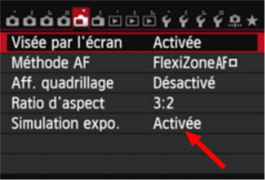
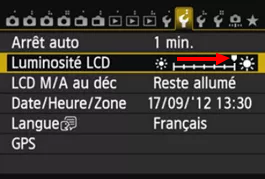
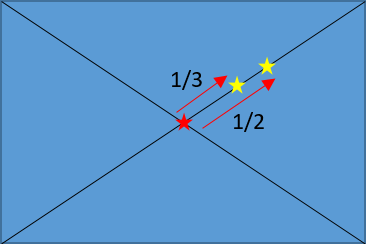
Tutoriel – Faire la mise au point de nuit On retrouve souvent la question « Comment fait-on la mise au point de nuit pour photographier la Voie Lactée ? ». Plein de mauvaises réponses sont proposées « utilise le repère infini de l’objectif », « règle toi à l’hyperfocale », « fait la mise au point de jour sur un objet éloigné, scotche l’objectif et attend la nuit »… En général, le résultat sera loin d’être optimum et la photo manquera vraiment de peps. Ce papier tente de fournir une procédure détaillée pour obtenir la meilleure mise au point possible. Cette procédure vous garantit d’avoir la meilleure mise au point possible à l’infini pour avoir des étoiles bien définies. Si vous cadrez un paysage en premier plan, celui-ci ne sera pas nécessairement net. J’en parle en seconde partie. Faire une vraie mise au point à l’infini Régler la luminosité de l’écran au maximum Ne conserver ce réglage que pour la mise au point et le cadrage. Dès que ces étapes sont effectuées, réglez la luminosité de l'écran au minimum, sinon en plus de vous cramer les yeux à chaque fois que vous regardez l'écran, vous aurez l'impression que vos photos sont bien exposées alors qu'elles seront sous exposées. Activer la Simulation d’exposition (quand c'est possible, voir nota ci-dessous) Cela permet à l’image affichée sur le LiveView d’être approximativement aussi lumineuse que ce que les réglages pose/ouverture/ISO le permettent. Nota : ce réglage n'est pas possible avec les boîtiers grand public, comme les Canon à 2, 3 et 4 chiffres (ex. 70D, 500D, 1300D...), elle est dans ce cas est toujours activée. Si vous avez un boitier plus haut de gamme, il est possible que la simulation d'exposition ne soit pas activée par défaut (Canon 6D par exemple). Régler les ISO, temps de pose et ouverture au maximum Par exemple sur un Canon 6D, monter à 12800 ISO, 30 s et sur un objectif f/2.8, mettre l’ouverture à f/2.8. L’idée est d’avoir l’image la plus lumineuse possible à l’écran du LiveView. Si l’image est trop lumineuse (à cause de la pollution lumineuse), baisser les ISO. Attention avec les objectifs à ouverture manuelle : régler dès ce stade l’ouverture à la valeur de vos futures prises de vues, car il ne faut plus toucher à l’objectif une fois la mise au point effectuée. Vérifier que l’objectif est bien en mode « mise au point manuelle (MF) » et désactiver la stabilisation. Placer la bague de mise au point l’objectif sur le repère infini C’est pour avoir une assez bonne approximation de la mise au point. On l’affinera plus tard. Viser à l’œilleton une étoile ou une planète lumineuse (mais pas la Lune !) peu importe sa position dans le ciel, elle ne sert qu’à faire la mise au point. Lancer le Live View sans zoomer. Chercher l’étoile visée. Il faut bien la centrer sur l’image. Affiner la mise au point pour qu’elle paraisse bien nette. Grossir le Live View x5 et rectifier la mise au point Grossir le Live View x10 et rectifier la mise au point Lorsque la focale de l'objectif est supérieure à environ 35 mm, vous pouvez essayer de viser Jupiter. Lorsque la mise au point est correcte, vous distinguerez alors les satellites galiléens en chapelet autour de la planète. Si vous avez des problèmes de vision, et donc du mal à voir l'étoile sur l'écran, n'hésitez pas à utiliser une loupe, les autres peuvent s’en passer. En ce qui me concerne, comme je deviens de plus en plus bigleux, il va falloir que j'investisse dans une petite loupe de poche. Une loupe éclairée permet aussi d'illuminer temporairement les boutons de l'appareil photo. Voilà, la mise au point est faite, il reste à : Cadrer le paysage Remettre la luminosité de l’écran à la valeur la plus faible Régler les ISO, temps de pose et ouverture aux valeurs souhaitées. Tant que vous ne touchez pas à votre objectif, il y a peu de chance que la mise au point change. Cela peut cependant arriver quand il y a une forte variation de température, disons de plus de 5-6°C, surtout avec les longues focales (>200 mm), il faut penser à refaire la mise au point régulièrement. Attention aux téléobjectifs à pompe qui ont souvent tendance à bouger tous seuls quand l’objectif est dirigé vers le haut ou vers le bas. Si cela arrive, il faut recommencer la procédure de mise au point. Comment faire avec les objectifs qui ont de fortes aberrations Certains objectifs présentent de fortes aberrations optiques (sphéricité, coma...) et si une étoile parait bien nette au centre, plus on s'en éloigne, plus les étoiles sont déformées, jusqu'à devenir de la bouillabaisse dans les angles. C'est souvent le cas avec les Samyang/Rokinon. Il est alors préférable de ne pas ajuster la mise au point au centre de l'image, mais environ au tiers ou à la moitié d'une diagonale partant du centre. De cette façon, l'image paraîtra plus homogène, même si les étoiles du centre ne seront pas parfaitement nettes. Il faudra tester car cela dépend de l'objectif. Faire la mise au point du paysage Le paysage n’est généralement pas à l’infini, surtout si des objets placés à quelques mètres de vous sont cadrés dans la photo. Dans cette situation, vous devrez prendre une série d’images pour le ciel, en suivant la procédure de mise au point à l’infini déjà expliquée, et une seconde série avec la mise au point sur le paysage. Vous combinerez ensuite les deux en post traitement en « focus stacking ». Pour faire la mise au point, reprendre les étapes 1 à 4 ci-dessus, puis : Placer la bague de mise au point approximativement à la distance de votre objet sur lequel doit être faite la mise au point, servez-vous de l’échelle de distance. Éclairer l’objet du paysage avec une torche puissante. Lancer le Live View, zoomer au maximum, et ajuster la mise au point manuellement La mise au point est maintenant faite, vous pouvez changer les réglages ISO, pose, ouverture à votre convenance, et affiner le cadrage. Ceux qui savent comment faire peuvent aussi faire la mise au point à l'hyperfocale. Pourquoi le réglage sur le repère infini de l’objectif n’est pas une bonne idée ? Quand on utilise la procédure décrite ci-dessus pour faire correctement la mise au point, on se rend compte qu’il suffit généralement d’une toute petite rotation de la bague de mise au point pour que la netteté soit perdue. Cette petite rotation est souvent si faible que la précision de gravure de l’échelle des distances sur l’objectif n’est vraiment pas suffisante. De plus les tolérances de fabrication et de calibration des objectifs font que le repère infini est très rarement au bon endroit. Il s’agit cependant d’une bonne valeur de départ pour avoir une image « à peu près nette » avant d’affiner la mise au point. Par contre, l’échelle de distance est généralement valable pour le paysage du premier plan. Pourquoi faire la mise au point de jour puis scotcher l’objectif n’est pas une bonne idée ? Le cerveau humain est plus tolérant sur la netteté d’un objet complexe comme un paysage que sur un ciel étoilé. Ainsi, alors que la netteté paraissait bonne de jour, il y a peu de chance qu'elle soit parfaite sur une étoile la nuit. De plus, scotcher l’objectif nécessite de toucher à la bague de mise au point, au risque de la bouger – et il ne faut pas grand-chose pour perdre la netteté. Enfin, vous allez probablement trimbaler votre appareil photo entre le réglage de jour et son utilisation de nuit, au risque là encore de bouger un peu la netteté. Pourquoi le réglage à l’hyperfocale n’est pas une bonne idée ? L’hyperfocale est une notion subjective. Tout repose sur la tolérance qu'ont l’œil humain et le cerveau pour déclarer qu’une image est nette ou floue. Cette tolérance est appelée « cercle de confusion » : un détail en théorie ponctuel, dont le diamètre sur le tirage (papier, écran) est inférieur à une certaine dimension sera considéré comme net. Évidemment plus on observe la photo de loin, plus ce cercle de confusion sera large. Au contraire, plus on observe la photo de près, plus il sera serré. Mais si le cerveau accepte qu’un détail d’un paysage ne soit pas exactement net, il n’en va pas de même avec les étoiles. Voilà pourquoi on ne parle pas d’hyperfocale avec les photos du ciel de nuit, le cerveau s’attend vraiment à y trouver des détails ponctuels, il faut donc que les étoiles soient le plus nettes possible. Par contre, vous pouvez très bien utiliser le réglage à l’hyperfocale pour le paysage du premier plan. Utilisation d'un masque de Bahtinov On peut utiliser un masque de Bahtinov pour aider la mise au point. J'en ai fabriqué un qui fonctionne plutôt bien À CONDITION d’avoir des focales supérieures à 40-50 mm environ (en dessous on ne voit pas les aigrettes). Le fil de discussion se trouve à ce lien. Le problème que j'ai rencontré est qu'il faut retirer le masque avant les prises de vues, et cela fait souvent bouger l'objectif même en faisant très attention. On perd tout l'intérêt du masque. Finalement je ne l'utilise jamais.